cos(x), cosine function.
Although the sine function is probably the most familiar of the six modern trigonometric functions, the cosine function comes a close second. Indeed, the sine and cosine functions are very closely related, as we shall see (if you are not familiar with the sine function, you may wish to read the page entitled "The Sine Function"). However, whereas the modern sine function is closely related to the chord function used by the ancient Greeks, the cosine function has no equivalent in Greek trigonometry. In fact, the Greeks had no other trigonometric functions apart from the chord.
Nevertheless, they were aware of the association between the sine and the cosine functions, albeit not in a trigonometric sense. The way in which the two functions relate to each other is captured in geometric terms by the Pythagorean theorem, which defines the relationship between the sides of a right-angled triangle. Consider the illustration below.
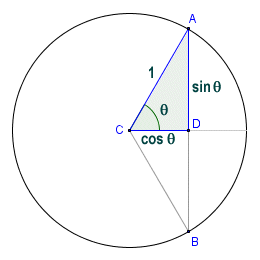
The relationship between sine and cosine
- Definition of cosine
- Graph of cosine
- Cosine rules
- Inverse cosine function
- Cosine table
- Cosine calculator
Cosine definition
In a right triangle ABC the sine of α, sin(α) is defined as the ratio between the side adjacent to angle α and the side opposite to the right angle (hypotenuse):
cos α = b / c
Example
b = 3"
c = 5"
cos α = b / c = 3 / 5 = 0.6
If you ask a calculator to find the arc cosine (cos-1 or acos) of a number, it cannot return an infinitely long list of angles, so by convention it returns just the first one. But remember, there are many others.
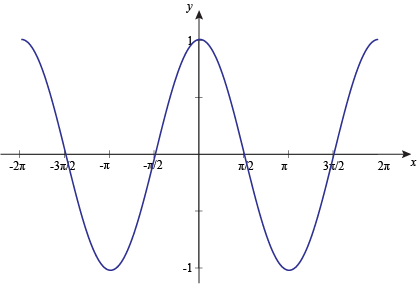
Graph of cosine

To graph the cosine function, we mark the angle along the horizontal x axis, and for each angle, we put the cosine of that angle on the vertical y-axis. The result, as seen above, is a smooth curve that varies from +1 to -1. It is the same shape as the cosine function but displaced to the left 90°. Curves that follow this shape are called 'sinusoidal' after the name of the sine function whose shape it resembles.
In the diagram above, drag the point A around in a circular path to vary the angle CAB. As you do so, the point on the graph moves to correspond with the angle and its cosine. (If you check the "progressive mode" box, the curve will be drawn as you move the point A instead of tracing the existing curve.)
The domain of the cosine function
As you drag the point A around notice that after a full rotation about B, the graph shape repeats. The shape of the cosine curve is the same for each full rotation of the angle and so the function is called 'periodic'. The period of the function is 360° or 2π radians. You can rotate the point as many times as you like. This means you can find the cosine of any angle, no matter how large. In mathematical terms we say the 'domain' of the cosine function is the set of all real numbers.
Range
The range of a function is the set of result values it can produce. The cosine function has a range that goes from -1 to +1. Looking at the cosine curve you can see it never goes outside this range.
Cosine rules
| Rule name | Rule |
|---|---|
| Symmetry | cos(-θ) = cos θ |
| Symmetry | cos(90°- θ) = sin θ |
| Pythagorean identity | sin2(α) + cos2(α) = 1 |
| cos θ = sin θ / tan θ | |
| cos θ = 1 / sec θ | |
| Double angle | cos 2θ = cos2 θ - sin2 θ |
| Angles sum | cos(α+β) = cos α cos β - sin α sin β |
| Angles difference | cos(α-β) = cos α cos β + sin α sin β |
| Sum to product | cos α + cos β = 2 cos [(α+β)/2] cos [(α-β)/2] |
| Difference to product | cos α - cos β = - 2 sin [(α+β)/2] sin [(α-β)/2] |
| Law of cosines | |
| Derivative | cos' x = - sin x |
| Integral | ∫ cos x dx = sin x + C |
| Euler's formula | cos x = (eix + e-ix) / 2 |
Inverse cosine function
The arccosine of x is defined as the inverse cosine function of x when -1≤x≤1.
When the cosine of y is equal to x:
cos y = x
Then the arccosine of x is equal to the inverse cosine function of x, which is equal to y:
arccos x = cos-1 x = y
Example
arccos 1 = cos-1 1 = 0 rad = 0°
See: Arccos function
The graph of the inverse cosine function is a lot like the graph of the inverse sine function. They're tight like that. It needs to be chopped into pieces, too, in order to pass the vertical line test. Poor inverse trig functions. They never get to be themselves.
To graph the inverse cosine function, we limit or choose a section of our regular cosine graph to work with. Here's y = cos x.
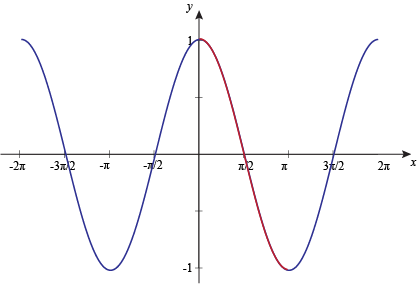
Next, we limit the domain to [0°, 180°], or [0, π] if you're feeling radian-y.
To find the inverse cosine graph, we have to swap the variables, which gives us:
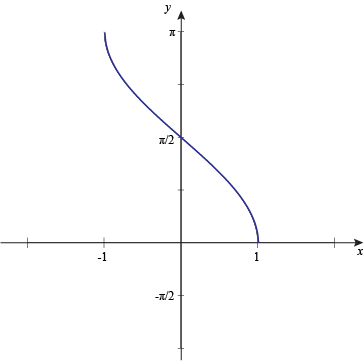
Inverse cos has a domain of [-1, 1] and a range of [0°, 180°], or [0, π].
That limits us to Quadrant I and Quadrant II when we're solving problems with the inverse cosine function.
Cosine table
| x (°) |
x (rad) |
cos x |
|---|---|---|
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
And now the main question. When do we use Cosine function?
Cos function is often used in excel as a mathematical function that calculates the Cos value of any angle. As we know, Cos angle is the ratio of Base to Hypotenuse, but in excel, we need to select radians function here along with COS Function to get the proper angle value. Also, we can multiply the input angel value with Pi()/180 other than using the Radians function.
The cosine function, along with sine and tangent, is one of the three most common trigonometric functions. In any right triangle, the cosine of an angle is the length of the adjacent side (A) divided by the length of the hypotenuse (H). In a formula, it is written simply as 'cos'.
Currently, we have around 5674 calculators, conversion tables and usefull online tools and software features for students, teaching and teachers, designers and simply for everyone.
You can find at this page financial calculators, mortgage calculators, calculators for loans, calculators for auto loan and lease calculators, interest calculators, payment calculators, retirement calculators, amortization calculators, investment calculators, inflation calculators, finance calculators, income tax calculators, compound interest calculators, salary calculator, interest rate calculator, sales tax calculator, fitness & health calculators, bmi calculator, calorie calculators, body fat calculator, bmr calculator, ideal weight calculator, pace calculator, pregnancy calculator, pregnancy conception calculator, due date calculator, math calculators, scientific calculator, fraction calculator, percentage calculators, random number generator, triangle calculator, standard deviation calculator, other calculators, age calculator, date calculator, time calculator, hours calculator, gpa calculator, grade calculator, concrete calculator, subnet calculator, password generator conversion calculator and many other tools and for text editing and formating, downloading videos from Facebok (we built one of the most famous Facebook video downloader online tools). We also provide you online downloanders for YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok and other social media sites (please note we does not host any videos on its servers. All videos that you download are downloaded from Facebook's, YouTube's, Linkedin's, Instagram's, Twitter's, Snapchat's, TikTok's CDNs. We also specialise on keyboard shortcuts, ALT codes for Mac, Windows and Linux and other usefull hints and tools (how to write emoji online etc.)
There are many very usefull online free tools and we would be happy if you share our page to others or send us any suggestions for other tools which will come on your mind. Also in case you find any of our tools that it does not work properly or need a better translation - please let us know. Our tools will make your life easier or simply help you to do your work or duties faster and in more effective way.
These below are the most commonly used by many users all over the world.
- Free online calculators and tools
- Time zones/Clocks/Dates calculators
- Free Online Units Conversion Calculators
- Free online web design tools
- Free online electricity & electronics tools
- Mathematics
- Online Tools
- Text Tools
- PDF Tools
- Code
- Ecology
- Others
- Free online downloaders for social media
- Marketing
- My PC / computer
- Numbers
- Algebra
- Trigonometry
- Probability & Statistics
- Calculus & analysis
- Mathematical symbols
- Arccos of 3
- Arccos of 0
- Arccos of 1
- Arccos of 2
- Arccos of cos(x)
- Arccos of sin(x)
- Arccos(x) derivative
- Arccos(x) function
- Arccos(x) graph
- Arcsin derivative
- Arcsin function
- Arcsin graph
- Arcsin integral
- Arcsin of 0
- Arcsin of 1
- Arcsin of infinity
- Arctan graph
- Arctan of 0
- Arctan of 1
- Arctan of 2
- Arctan of infinity
- Arctangent function
- Cos of arccos(x)
- Cos of arcsin
- Cosine function
- Cosine of arctan(x)
- Derivative of arctan
- Integral of arctan
- Sin of arccos(x)
- Sin of arcsin
- Sine function
- sine of arctan(x)
- Tan of arccos(x)
- Tan of arcsin
- Tangent function
And we are still developing more. Our goal is to become the one-stop, go-to site for people who need to make quick calculations or who need to find quick answer for basic conversions.
Additionally, we believe the internet should be a source of free information. Therefore, all of our tools and services are completely free, with no registration required. We coded and developed each calculator individually and put each one through strict, comprehensive testing. However, please inform us if you notice even the slightest error – your input is extremely valuable to us. While most calculators on Justfreetools.com are designed to be universally applicable for worldwide usage, some are for specific countries only.