What is factorial (n!)
When you saw an exclamation point in maths for the first time, you probably got shocked or even thought that there was some kind of mistake or typo. But the reality is different: this exclamation point in maths is called the factorial or n-factorial. The factorial is a reasonably unknown operator that can, in fact, be viewed more as an abbreviation than an actual operator, at least at the beginning.
It is important not to confuse the factorial with the prime factorization of a number, which is a way of obtaining the prime numbers that, when multiplied together, give your number. Prime factorization has its uses in maths and is arguably more well known than the n-factorial. Part of the reason for the popularity of prime factorization is its usefulness when calculating Greatest Common Factor (GCM) and the Least Common Multiplier (LCM), but we digress.
To understand what the factorial does or means, we should start with an example. We could choose any number n and calculate its n-factorial value, but it's best to choose a relatively small number, so let's use 5-factorial.
5! = 5 * 4 * 3 * 2 * 1 = 120
From this example, you can see that it is not rocket science, and you might even take a guess at the factorial formula. You can also understand why this exclamation point in maths can be regarded as an abbreviation since it is not a new operation but rather a collection of multiplications. In short, and somewhat informally, we can define the factorial as the multiplication of all the positive integers smaller than and equal to the given number.
Playing a bit with this, we can see that for 5-factorial, we can relate it to the 4-factorial in a straightforward way:
5! = 5 * (4 * 3 * 2 * 1) = 5 * 4!
This kind of relationship between n-factorials with a different n is the basis of the mathematical formula that defines the factorial operation, as we will see in the next section.
The factorial operation is not used everywhere in maths, but it is essential in statistics and probability problems. In those cases, especially when one has to deal with permutations or combinatorics, the n-factorial appears almost all the time. In the following sections of our factorial calculator, we will see real-world examples of problems that require the usage of factorials and the factorial formula.
So the factorial of n is denoted by n! and calculated by the product of integer numbers from 1 to n.
For n>0,
n! = 1×2×3×4×...×n
For n=0,
0! = 1
Factorial definition formula
Examples:
1! = 1
2! = 1×2 = 2
3! = 1×2×3 = 6
4! = 1×2×3×4 = 24
5! = 1×2×3×4×5 = 120
Recursive factorial formula
n! = n×(n-1)!
Example:
5! = 5×(5-1)! = 5×4! = 5×24 = 120
Stirling's approximation
Example:
5! ≈ √2π5⋅55⋅e-5 = 118.019
Factorial table
| Number n |
Factorial n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 3.991680x107 |
| 12 | 4.790016x108 |
| 13 | 6.227021x109 |
| 14 | 8.717829x1010 |
| 15 | 1.307674x1012 |
| 16 | 2.092279x1013 |
| 17 | 3.556874x1014 |
| 18 | 6.402374x1015 |
| 19 | 1.216451x1017 |
| 20 | 2.432902x1018 |
C program for factorial calculation
double factorial(unsigned int n)
{
double fact=1.0;
if( n > 1 )
for(unsigned int k=2; k<=n; k++)
fact = fact*k;
return fact;
Explanation of zero factorial
We can understand why many of us have a hard time accepting the fact that the value of zero factorial is equal to one. It comes across as an absurd statement that there’s no way it can be true. We have a common perception of zero for being notorious because there’s something about it that can make any number associated with it either vanish or misbehave.
For instance, a large number such as 1,000 multiplied by zero becomes zero. It disappears! On the other hand, a nice number such as 5 divided by zero becomes undefined. It misbehaves. So it is okay to be skeptical why zero “suddenly” becomes one, a nice number, after treating it with some special operation.
There are other ways to show why the statement is true. For this one, we will use the definition of factorial itself. To be honest, with this method the justification is simple and requires little math.
Let be a whole number, where is defined as the product of all whole numbers less than and including itself.
What it means is that you first start writing the whole number then count down until you reach the whole number .
The general formula of factorial can be written in fully expanded form as
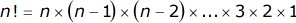
or in partially expanded form as
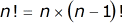
We know with absolute certainty that 1!=1, where . If we substitute that value of into the second formula which is the partially expanded form of , we obtain the following:
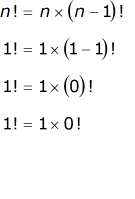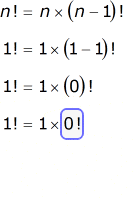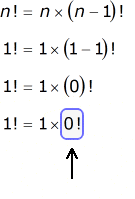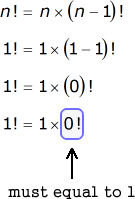
For the equation to be true, we must force the value of zero factorial to equal 1, and no other. Otherwise, 1!≠1 which is a contradiction.
So yes, 0! = 1 is correct because mathematicians agreed to define it that way (nothing more and nothing less) in order to be consistent with the rest of mathematics. (Source: Chilimath.com)
Currently, we have around 5674 calculators, conversion tables and usefull online tools and software features for students, teaching and teachers, designers and simply for everyone.
You can find at this page financial calculators, mortgage calculators, calculators for loans, calculators for auto loan and lease calculators, interest calculators, payment calculators, retirement calculators, amortization calculators, investment calculators, inflation calculators, finance calculators, income tax calculators, compound interest calculators, salary calculator, interest rate calculator, sales tax calculator, fitness & health calculators, bmi calculator, calorie calculators, body fat calculator, bmr calculator, ideal weight calculator, pace calculator, pregnancy calculator, pregnancy conception calculator, due date calculator, math calculators, scientific calculator, fraction calculator, percentage calculators, random number generator, triangle calculator, standard deviation calculator, other calculators, age calculator, date calculator, time calculator, hours calculator, gpa calculator, grade calculator, concrete calculator, subnet calculator, password generator conversion calculator and many other tools and for text editing and formating, downloading videos from Facebok (we built one of the most famous Facebook video downloader online tools). We also provide you online downloanders for YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok and other social media sites (please note we does not host any videos on its servers. All videos that you download are downloaded from Facebook's, YouTube's, Linkedin's, Instagram's, Twitter's, Snapchat's, TikTok's CDNs. We also specialise on keyboard shortcuts, ALT codes for Mac, Windows and Linux and other usefull hints and tools (how to write emoji online etc.)
There are many very usefull online free tools and we would be happy if you share our page to others or send us any suggestions for other tools which will come on your mind. Also in case you find any of our tools that it does not work properly or need a better translation - please let us know. Our tools will make your life easier or simply help you to do your work or duties faster and in more effective way.
These below are the most commonly used by many users all over the world.
- Free online calculators and tools
- Time zones/Clocks/Dates calculators
- Free Online Units Conversion Calculators
- Free online web design tools
- Free online electricity & electronics tools
- Mathematics
- Online Tools
- Text Tools
- PDF Tools
- Code
- Ecology
- Others
- Free online downloaders for social media
- Marketing
- My PC / computer
- Numbers
- Algebra
- Trigonometry
- Probability & Statistics
- Calculus & analysis
- Mathematical symbols
- Derivative of logarithm
- Factorial
- Logarithm
- Logarithm change of base rule
- Logarithm of Infinity
- Logarithm of negative number
- Logarithm of one
- Logarithm of zero
- Logarithm rules
- Natural logarithm
- Quadratic equation
And we are still developing more. Our goal is to become the one-stop, go-to site for people who need to make quick calculations or who need to find quick answer for basic conversions.
Additionally, we believe the internet should be a source of free information. Therefore, all of our tools and services are completely free, with no registration required. We coded and developed each calculator individually and put each one through strict, comprehensive testing. However, please inform us if you notice even the slightest error – your input is extremely valuable to us. While most calculators on Justfreetools.com are designed to be universally applicable for worldwide usage, some are for specific countries only.